堀口です。今日は、とあるユニークな問題を考えたいと思います。
Q.山手線に乗ったら隣に友人が乗っている確率は?
山手線に乗ったら隣に友人がくる確率は?ふと席についた瞬間隣に友人がいたら驚きますよね?
今日はそんな驚きの確率を計算してみたいと思いますが・・・
まずこの問題ですが、非常に難しいです。真面目に考えてしまうと、考えるべき事柄が多く、とても解説できる気がしません。このテーマだけで何本かの論文になる気がします(笑)
まずは私なりの仮定をたくさん置く中でつくった、誰でも理解しやすいようなモデルで、解説したいと思います。
解説例(超単純モデル)
まず、仮定をおきます。
・東京の人口は約1400万人。
・友人の人数を150人くらいとする。(ダンバー数(※)より設定。)
・友人は全員東京の人。
・山手線の1日あたりの乗降客数を400万人とする。(週の乗降客数が約3000万人であることから設定。(※))
・山手線に乗る人は、全員東京の人。
・山手線に乗ったら自分以外全員席に座っている。(自分が席に座れて両隣にも人がいる)つまり、山手線の席に座ったら両側に友人がいる可能性がある。(実際のところは、席によっては片側のみの場合もあります。)
ここからちょっとだけ計算を入れます。
・山手線に乗る人は、行きと帰りで、1日2回乗る。つまり、200万人乗っている。
・山手線に200万人乗っているということは、7人中1人(東京の人が1400万人いるので。)つまり、自分の友人の約20人が乗っている計算。
ここから大胆にさらに仮定します。
乗っている時間帯やどの車両に乗るか。人の入れ替えなど、考えるべき事項が非常に多いので、もう山手線に1日の中で乗るであろう人をすべて横一列に並べます。
意味が分かりにくいかもしれませんが、普通はこういう配置です。
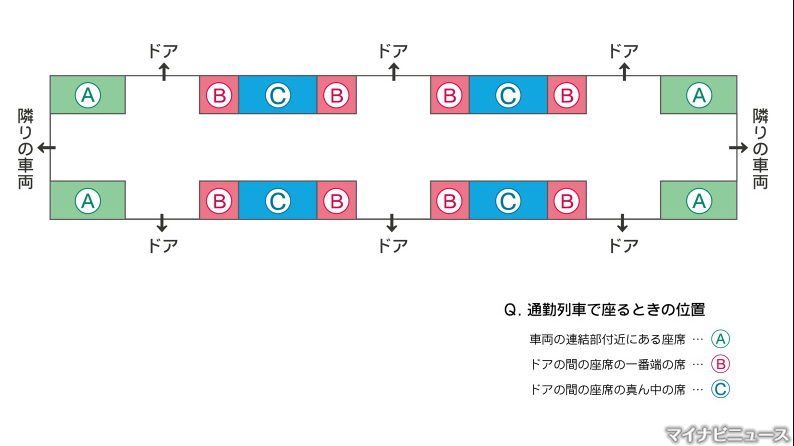
これを一列にくっつけます。イメージ的にはこんな感じです。
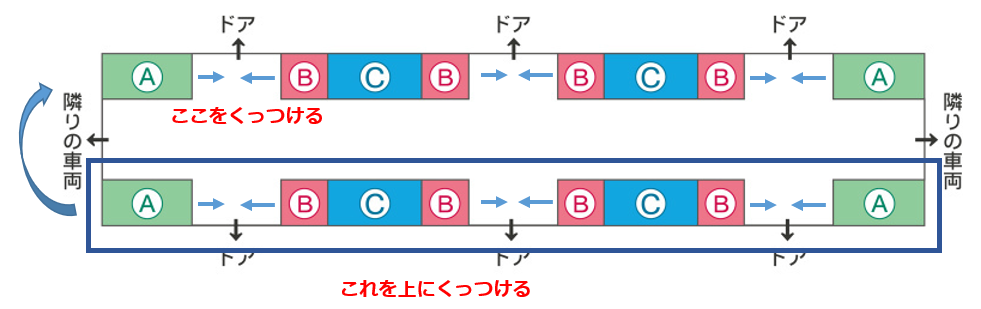
大胆に、こんな感じです。
こうやって、一列に並べたときに自分の隣に友人がくる確率を考えます。
そうすると、約200万人のうち、約20人の友人が山手線に乗っているということになりますから、このとき、単純計算で右隣りに自分の友人がいる確率が、約10万人に1人なわけですから、10万分の1になります。
今回は”両隣”を考えていますから、右と左で確率はその2倍。5万分の1という計算式になります。
非常にざっくりですが、こんな形で求めることができます。
いかがでしょうか?
5万分の1の意味とは
山手線で隣の席に友人が座っている確率は5万分の1。これは相当小さく、人の一生80年と考えると、約3万日。1日2回電車に乗るとして、一生にようやく1回くらい起こるという感じでしょうか。
もちろん、現実問題、友人の通勤ルートが一緒だったりするともっと確率は高くなりますし、山手線に何度も乗ったり、隣の席じゃなくて同じ車両では?・・と拡張して考えていくと全く違う確率になっていくと思います。
今回の解き方は、数理モデルを考えているというよりは、フェルミ推定的な解き方でした。
この問題、非常に深いので、ぜひ挑戦者をお待ちしております。
こういう問題をわかりやすく、かつ、厳密に求めることができる選手権とか面白そうですね(笑)実は、和からの優秀なスタッフもこの問題挑戦しており、他のパターンでも答えを出しております。
実はこの問題・・・
某テレビ局からの依頼でものすごい時間をかけて様々なパターンの答えの出し方を検討していたのですが、なんと全カットされたということで公開にいたりました。どこまで仮定するか、どの程度の知識の人に解説するかを考えなければより精度高く求めることができますが非常に難しくなってきます。
テレビ局の方おりましたら、オファーお待ちしております(笑)
参考URL
・ダンバー数-wikipedia
・首都圏路線群と延べ利用者数/平均乗車時間(PDF)
<文/堀口智之>