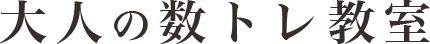さて、先日、ピタゴラス音律について記事を書きました。(引用:ピタゴラス音律に見る音楽と数学の関係性)
つまりは、周波数が1:2、2:3、3:4など最小公倍数が小さくなるような整数比のときにキレイなハーモニーとなるという話でした。これらの振動数を実際に足し合わせてみた波形がどのようになるかを眺めていきたいと思います。
「美しい!」
と感じて頂ければ幸いです。視覚的に楽しむこと、グラフで見たときにどんな感じになるかを鑑賞していただければ幸いです。
「ド」と「ソ」
周波数が2:3になるときにどのようなグラフになるか眺めてみましょう。音程としては完全5度です。(周波数が2:3ということは、波長はその逆数となりますので、3:2の比率となります。詳しい説明はここでは省きます。)
まずこちらの周波数と
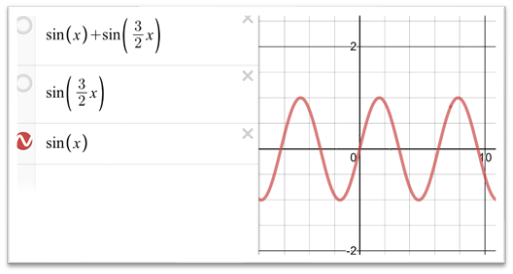
こちらの周波数が同時に鳴るので
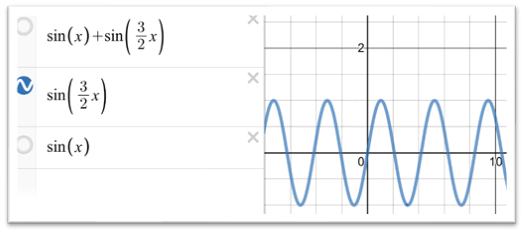
このようなグラフとなります。
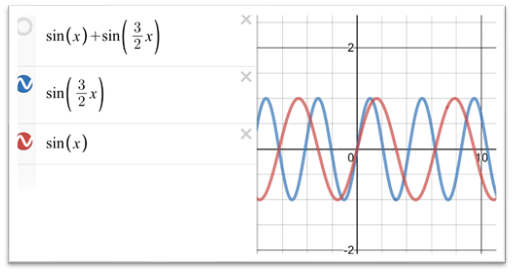
実際に足し合わせてみると、
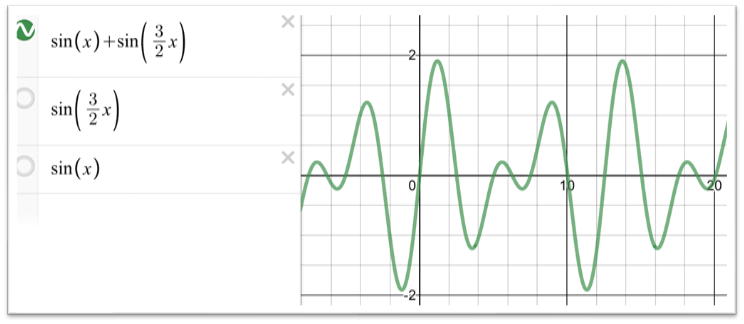
こんなグラフとなります。実際に鳴らしていただけるとわかるのですが、非常に美しい音です。ピタゴラスもこの音の響きの美しさに魅了されていたと思われます。
「ド」と「ファ」
今度は周波数が3:4です。先ほどよりは美しさは劣りますが、それでも美しく響きます。実際にグラフで見てみましょう。音程としては完全4度です。

「ド」と「ミ」
今度は、周波数が4:5のとき。「ド」と「ミ」です。音程としては長3度です。カエルの歌の輪唱のときにこの音が同時になる瞬間をイメージしていただければその美しさはイメージしやすいかと思います。
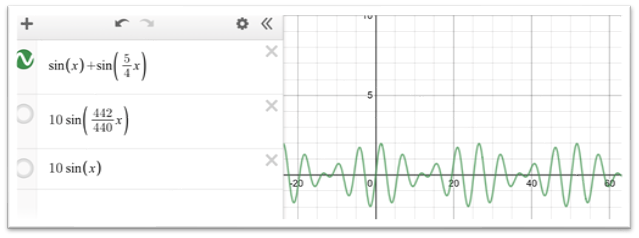
少しこのあたりから見えてきますが、一つ一つの波ではなく、4~5つの波で一つのサイクルの波を描いているのは見えるでしょうか。これを「うなり」と言います。実際のところ普通の音の高さは1秒間に500回程度の空気の振動となるので、このうなりは実際には聞こえません。
うなりをグラフで見てみる
もっと周波数が近いものだとよりわかりやすくなりますし、実際に聞こえます。例えば、このような形です。440:442という波長の長さの波を足し合わせてみるとこのようになります。
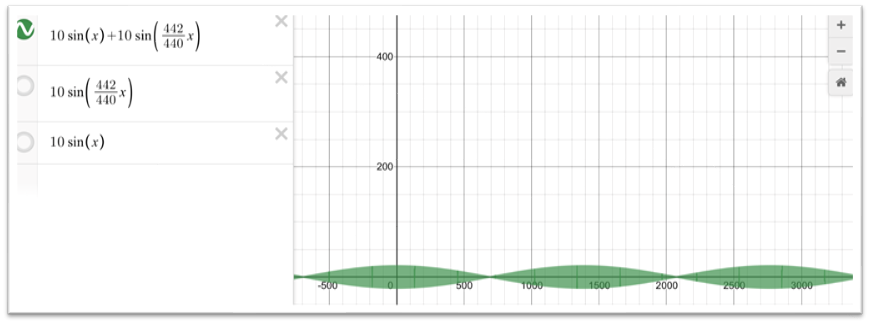
このうなりは聞こえます。
私自身もアコースティックギターなどで440Hzが鳴る音叉を用いて音の高さを合わせる、チューニングをしていました。
「うおーーーん、うおーーん」
という感じで音全体の大きさが大きくなったり、小さくなったりする微妙な変化が聞こえます。このうなりが聞こえないところがちょうどの音の高さがマッチするところなのです。
ただし、「うなりが聞こえない」というのは、同じ音に聞こえるということで、結構わかりにくいものです。だからこそ、音を高くしてうなりが聞こえて、音を低くしてからうなりが聞こえ、その真ん中くらいに調整するようにすると、同じ音程として調音することができるのです。
以上、楽しんでいただけましたか?
今回desmosというソフトを用いて表現しました。ぜひ気になる方はチェックしてみてください。(引用:グラフ計算機-desmos)
<文/堀口智之>